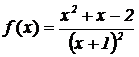Matemáticas aplicadas a las
Ciencias Sociales II Junio 2022
BAREMO
DEL EXAMEN:
Se
han de contestar tres problemas de entre los seis propuestos.
Cada problema se valorará de
Se permite el uso de calculadoras siempre
que no sean gráficas o programables, y que no puedan realizar cálculo simbólico
ni almacenar texto o fórmulas en memoria. Se utilice o no la calculadora, los
resultados analíticos, numéricos y gráficos deberán estar siempre debidamente
justificados. Está permitido el uso de regla. Las gráficas se harán con el
mismo color que el resto del examen.
Todas las respuestas han de estar debidamente
razonadas.
Problema 1. Una agencia inmobiliaria tiene tres
locales en alquiler, por los que ha cobrado en total 1650 euros en este mes. La
agencia ha pagado al propietario del primer local el 95% de la cantidad que ha
cobrado por su alquiler; al propietario del segundo local, el 90% de la
cantidad que ha cobrado por su alquiler; y al propietario del tercer local, el
80% de la cantidad que ha cobrado por su alquiler. Tras estos tres pagos, a la
agencia le han quedado 132 euros de ganancia. Se sabe también que el alquiler
que se cobra por el primer local es el doble de la suma de lo que se cobra por
el alquiler de los otros dos locales juntos. ¿Cuántos euros cobra la agencia
por cada uno de los tres locales que tiene en alquiler?
(Planteamiento correcto 5 puntos - Resolución correcta 5 puntos)
Problema 2. Una empresa apícola vende dos tipos de cajas
con tres variedades de miel en cada una: miel de romero, miel de azahar y miel
multifloral. La caja de tipo A contiene 2 tarros de miel de romero, 2 de azahar
y 1 de multifloral. La caja de tipo B contiene 1 tarro de miel de romero, 2 de
azahar y 2 de multifloral. Cada día la empresa dispone de 280 tarros de miel de
romero, 300 de miel de azahar y 250 de miel multifloral. Con cada caja de tipo
A obtiene un beneficio de 7 euros y con cada caja de tipo B obtiene un
beneficio de 5 euros.
a)
¿Cuántas cajas de cada tipo debe comercializar
para obtener un beneficio máximo?
(8 puntos)
b)
¿Cuál es dicho beneficio máximo? (2
puntos)
|
Problema 3.
Dada la función |
|
, se pide: |
a)
Su dominio y los puntos
de corte con los ejes coordenados. (2 puntos)
b)
Las asíntotas
horizontales y verticales, si existen. (2 puntos)
c)
Los intervalos de
crecimiento y decrecimiento. (2 puntos)
d)
Los máximos y
mínimos locales, si existen. (2 puntos)
e)
La representación
gráfica de la función a partir de los resultados anteriores. (2 puntos)
Problema 4. En
una empresa se ha comprobado que sus beneficios están relacionados con su
inversión en publicidad según la función
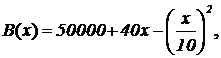
donde x es la inversión en
publicidad (x
≥ 0) y B(x) es el beneficio
obtenido, ambos en euros.
a)
Calcula la cantidad
invertida en publicidad que produce un beneficio máximo. ¿Cuál es dicho
beneficio máximo? (4 puntos)
b)
Calcula los
intervalos para la inversión en publicidad en los que los beneficios crecen o
decrecen a medida que se invierte en publicidad. (3
puntos)
c)
¿Existe
un valor para la inversión en publicidad a partir del cual los beneficios
obtenidos serían menores que si no se invirtiera nada en publicidad? En caso
afirmativo, determínalo. (3
puntos)
Problema 5. Entre
los clientes de una compañía de seguros de automóviles, un 30% tiene menos de
30 años, un 55% tiene entre 30 y 60 años, y el 15% restante tiene más de 60
años. Se sabe que, entre los clientes de menos de 30 años, 3 de cada 4 no
presentaron parte de accidente el año pasado; entre los clientes que tienen
entre 30 y 60 años, 9 de cada 10 no presentaron parte de accidente el año
pasado; y entre los clientes de más de 60 años, 2 de cada 5 no presentaron
parte de accidente el año pasado. Seleccionamos al azar un cliente de la
compañía.
a)
Llamemos A al
suceso “el cliente seleccionado tiene más de 60 años” y llamemos B al suceso
“el cliente seleccionado no presentó parte de accidente año pasado”. Calcula
P(A È B). (3
puntos)
b)
Llamemos C al
suceso “el cliente seleccionado tiene 30 años o más” y D al suceso “el cliente
seleccionado presentó parte de accidente el año pasado”. Calcula P(C∩D).
(3 puntos)
c)
Si sabemos que el
cliente seleccionado presentó parte de accidente el año pasado, calcula la
probabilidad de que tenga 60 años o menos. (4
puntos)
Problema 6. En
un juego se lanzan dos monedas equilibradas y un dado de seis caras
equilibrado. Un jugador gana si obtiene dos caras y un número par en el dado, o
bien, si obtiene exactamente una cara y un número mayor o igual que cinco en el
dado.
a)
Calcula
la probabilidad de que el jugador gane. (2´5
puntos)
b)
Si se sabe que ha
ganado, ¿cuál es la probabilidad de que obtuviera dos caras al lanzar las
monedas? (2´5
puntos)
c)
Si se sabe que ha ganado, ¿cuál es la probabilidad de
que obtuviera un cinco al lanzar el dado? (2´5
puntos)
d) Llamemos A al suceso “el jugador no gana” y llamemos
B al
suceso “el jugador obtiene un seis al lanzar el dado”. ¿Son independientes los
sucesos? (2´5 puntos)