Matemáticas aplicadas a las
Ciencias Sociales II Junio 2025 (reserva)
BAREMO
DEL EXAMEN: Se
ha de contestar un problema del Apartado 1, un problema del Apartado 2 y el
problema del Apartado 3.
En cada cuestión se
indica la puntuación máxima, siendo la nota final la suma de las calificaciones
de cada una ellas. Se permite el uso de calculadoras siempre que no sean
gráficas o programables y que no puedan realizar cálculo simbólico ni almacenar
texto o fórmulas en memoria. Se utilice o no la calculadora, los resultados
analíticos, numéricos y gráficos deberán estar siempre debidamente
justificados. Está permitido el uso de regla. Las gráficas se harán con el
mismo color que el resto del examen.
Todas las respuestas han de estar debidamente
razonadas.
Apartado 1. Responda un problema de este
apartado de los dos propuestos.
Problema 1.
A. En época de regalos navideños, con
225 euros se pueden comprar dos libros, tres plumas estilográficas y un reloj
inteligente. Sin embargo, en época de rebajas nos descuentan 5 euros de cada
artículo, lo que nos permite comprar un libro más con ese mismo dinero.
Después, en febrero, pasada la época de rebajas, cada artículo cuesta 5 euros
más que en la época navideña, de manera que, con ese mismo dinero, podemos
comprar tres plumas y tres libros, pero ningún reloj inteligente. ¿Cuál es el
precio del libro, de la pluma estilográfica y del reloj inteligente en época
navideña?
(Planteamiento correcto 1,5 puntos --- Resolución
correcta 2 puntos)
Problema
1. B. Un creador de contenido desea invertir en
publicidad hasta 10000 euros. Ha considerado dos empresas, A y B. La empresa
de publicidad A es más agresiva, y garantiza un incremento anual en número de
seguidores del 10% de lo que se invierte; la B es más tradicional y el
incremento en número de seguidores que garantiza es del 7% de lo que se
invierte. Así pues, el creador desea invertir al menos 2.000 euros en la
empresa B y un máximo de 6.000 euros en la A, invirtiendo siempre en la A al
menos lo invertido en la B.
a)
¿Cuánto
dinero tiene que asignar a cada empresa para que el incremento de seguidores
sea máximo? (3 puntos)
b)
¿Cuál
es dicho incremento de seguidores máximo? (0,5
puntos)
Apartado 2. Responda un problema de este
apartado de los dos propuestos.
Problema 2.
A. La temperatura, T, de un motor depende de las
revoluciones, r, del mismo de forma
que entre 0 y 100 revoluciones evoluciona siguiendo una tendencia lineal tal
que:
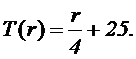
Sin embargo, a partir de 100 revoluciones la
temperatura depende del cuadrado de las revoluciones, de forma que: T(r) =A
r2 + B, siendo A y B
números reales.
Se pide:
a)
Teniendo
en cuenta que la función debe ser continua y que la derivada de T(r) en r = 1600
vale 4, determina A
y B. (1,5
puntos)
b)
¿Existen
máximos o mínimos para la temperatura en función de las revoluciones? Justifica
la respuesta. (1 punto)
c)
Un
operario utiliza el motor durante 30 minutos de forma que en el minuto m
las revoluciones que tiene el motor vienen dadas por la expresión r(m) =
5 m – 0´15 m2. Determina
en qué minutos las revoluciones son máximas y mínimas, el valor de estas y el
valor de la temperatura en esos momentos. (1
punto)
Problema 2.
B. Se considera la función:
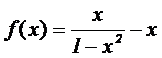
Se pide:
a)
Su
dominio y los puntos de corte con los ejes coordenados. (0,5 puntos)
b)
Las
asíntotas horizontales y verticales, si existen. (0,5 puntos)
c)
Los
intervalos de crecimiento y decrecimiento, y los máximos y mínimos locales, si
existen. (2 puntos)
d)
La
representación gráfica de la función a partir de los resultados obtenidos en
los apartados anteriores. (1
punto)
Apartado 3. Responda el único problema de este
apartado. (3 puntos)
Problema 3. Una prueba diagnóstica para detectar la artritis
reumatoide da positiva en el 96% de los casos cuando se tiene la enfermedad, y
da negativa en el 94% de los casos cuando no se tiene la enfermedad. Entre los
habitantes de un cierto pueblo, se sabe que uno de cada ciento cuarenta y cinco
tiene la enfermedad sin saberlo. Se escoge al azar un habitante de este pueblo
y se le aplica la prueba.
a)
Calcula la
probabilidad de que el habitante seleccionado padezca artritis reumatoide y la
prueba haya dado negativa. (1 punto)
b)
Si el resultado
de la prueba ha dado positivo, ¿cuál es la probabilidad de que el habitante
seleccionado padezca artritis reumatoide? (1 punto)
c)
Calcula la
probabilidad de que el resultado de la prueba sea correcto. (1 punto)