Matemáticas aplicadas a las
Ciencias Sociales II Julio 2025 Reserva
BAREMO
DEL EXAMEN: Se
ha de contestar un problema del Apartado 1, un problema del Apartado 2 y el
problema del Apartado 3.
En cada cuestión se
indica la puntuación máxima, siendo la nota final la suma de las calificaciones
de cada una ellas. Se permite el uso de calculadoras siempre que no sean
gráficas o programables y que no puedan realizar cálculo simbólico ni almacenar
texto o fórmulas en memoria. Se utilice o no la calculadora, los resultados
analíticos, numéricos y gráficos deberán estar siempre debidamente
justificados. Está permitido el uso de regla. Las gráficas se harán con el
mismo color que el resto del examen.
Todas las respuestas han de estar debidamente
razonadas.
Apartado 1. Responda un problema de este
apartado de los dos propuestos.
Problema 1. A. Esta semana una chica ha consumido 1.470 megabytes de datos de su móvil
conectándose a redes sociales, a periódicos y a la universidad. La chica ha
pasado 10 horas conectada a redes sociales, 4 horas conectada a periódicos y 6
horas conectada a la universidad. Se sabe que en una hora de conexión a redes
sociales se consume un 20% más de megabytes que en una hora de conexión a
periódicos. Se sabe también que en una hora de conexión a periódicos se consume
30 megabytes más que en una hora de conexión a la universidad. ¿Cuántos
megabytes consume una hora de conexión a redes sociales?; ¿cuántos una hora de
conexión a periódicos?; ¿cuántos una hora de conexión a la universidad?
(Planteamiento correcto 1,5 puntos ---
Resolución correcta 2 puntos)
Problema 1.
B. Consideramos las matrices
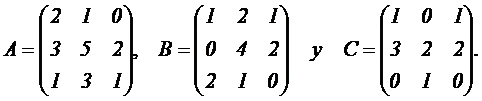
a)
Calcula el
producto A C t, siendo C t la matriz traspuesta de C. (0,75 puntos)
b)
Calcula la
inversa de la matriz B – A. (1,25 puntos)
c)
Obtén
la matriz X que verifica la ecuación X t A + C = X t B,
siendo X t la matriz traspuesta de X. (1,5 puntos)
Apartado 2. Responda un problema de este
apartado de los dos propuestos.
Problema 2.
A. El valor de una empresa (en millones de euros) se expresa en función del tiempo t
(en años) según la función B(t) = – t2 + 12 t – 11,
para t entre
2 y 9.
a)
¿En
qué momento alcanza la empresa su valor máximo y cuál es este valor?
(0´75 puntos)
b)
¿En
qué momento alcanza la empresa su valor mínimo y cuál es este valor?
(0´75 puntos)
c)
¿En
qué periodo el valor de la empresa es superior a 24 millones de euros?
(1´25 puntos)
d)
Calcula la siguiente integral: (0´75 puntos)
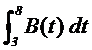
Problema 2.
B. Se considera la
función:
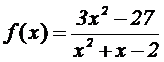
Se pide:
a)
Su
dominio y los puntos de corte con los ejes coordenados. (0,5 puntos)
b)
Las
asíntotas horizontales y verticales, si existen. (0,5 puntos)
c)
Los
intervalos de crecimiento y decrecimiento, y los máximos y mínimos locales, si
existen. (2 puntos)
d)
La
representación gráfica de la función a partir de los resultados obtenidos en
los apartados anteriores. (0,5
puntos)
Apartado 3. Responda el único problema de este
apartado. (3 puntos)
Problema 3. Una empresa de mantenimiento de automóviles evalúa los
coches haciéndoles dos controles; si los dos salen negativos entonces el coche
se califica como no adecuado y si los dos salen positivos entonces se califica
como adecuado. Sin embargo, si uno de los controles sale positivo y el otro
negativo, entonces se le hace un tercer control; si este sale positivo la
calificación es de coche adecuado, y en caso contrario la calificación es de no
adecuado. Se sabe que una determinada marca pasa correctamente el primer
control con una probabilidad de 0,8 y que la probabilidad de que pase el
control disminuye en 0,1 cada vez que se le hace un control. Seleccionamos al
azar un coche de esta marca para su evaluación.
a)
¿Cuál es la
probabilidad de que el coche seleccionado sea calificado como adecuado? (1 punto)
b)
Si se sabe que el
coche seleccionado ha sido calificado como adecuado, ¿cuál es la probabilidad
de que haya pasado el primer control? (1 punto)
c)
Si se sabe que al
coche seleccionado solo se le han hecho dos controles, ¿cuál es la probabilidad
de que haya sido calificado como adecuado? (1 punto)