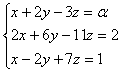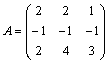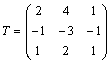Matemáticas II Junio 2006
Baremo:
Se elegirá el
EJERCICIO A o el EJERCICIO B, del que sólo se harán TRES de los problemas propuestos.
Cada problema se puntuará de 0 a 3,3, según la puntuación máxima indicada en
cada apartado.
La suma de las
puntuaciones de cada problema más 0,1 será la calificación de la prueba.
Cada estudiante
deberá disponer de una calculadora científica o gráfica para la realización del
examen. Se prohíbe su utilización indebida (para guardar fórmulas en memoria).
EJERCICIO A
|
PROBLEMA 1. Dado el sistema de ecuaciones con incógnitas x , y, z, |
|
se
pide:
a)
Determinar
razonadamente el valor de ![]() para el cual el
sistema es compatible (1,2 puntos).
para el cual el
sistema es compatible (1,2 puntos).
b)
Para ese valor
obtenido en a) de ![]() , calcular el conjunto de soluciones del sistema (1,3 puntos).
, calcular el conjunto de soluciones del sistema (1,3 puntos).
c)
Explicar la
posición relativa de los tres planos definidos por cada una de las tres
ecuaciones del sistema, en función de los valores de ![]() (0,8 puntos).
(0,8 puntos).
PROBLEMA 2. En el espacio se consideran:
La
recta r
intersección de dos planos de ecuaciones implícitas: x + y – z = 5 y
2 x + y – 2 z = 2 .
Y
la recta s que pasa por los puntos P = (3, 10, 5)
y Q = (5, 12, 6). Se pide:
a)
Calcular las ecuaciones
paramétricas de la recta r (0,6
puntos) y de la recta s (0,4
puntos).
b)
Calcular el
punto H
intersección de r y s (0,6
puntos) y el ángulo ![]() que determinan r
y s (0,4
puntos).
que determinan r
y s (0,4
puntos).
c)
Calcular los
puntos M
y N de la recta
r para los que el área de cada
uno de los triángulos de vértices
PQM y PQN
es 3 unidades de área (1,3 puntos).
PROBLEMA 3.
a)
Dibujar
razonadamente la gráfica de la función
g(x) = x2 – 4, cuando -1 ≤ x ≤ 4 (1,1 puntos).
b)
Obtener
razonadamente los valores máximo y mínimo absolutos de la función f(x) = │ x2 – 4│ en el
intervalo [-1, 4] (1,1 puntos).
c)
Calcular el área
del recinto limitado por la curva de ecuación
y = f(x) y las rectas x = – 1 ,
x = 4 e y = 0 (1,1
puntos).
PROBLEMA 4. Una persona camina a la velocidad constante de 3m/s
alejándose horizontalmente en línea recta desde la base de un farol cuyo foco
luminoso está a 10 m de altura. Sabiendo que la persona mide 1,70 m, calcular:
a)
La longitud de la
sombra cuando la persona está a 5 m de la base del farol (2
puntos).
b)
La velocidad de
crecimiento de la sombra a los t segundos de comenzar a caminar (1,3 puntos).
EJERCICIO B
|
PROBLEMA 1. Dadas las matrices |
|
y |
|
se
pide |
a)
Probar que la
matriz T tiene matriz inversa, T-1
, y calcular dicha matriz inversa T-1
(1,3 puntos).
b)
Dada la ecuación
con matriz incógnita B, A = T-1 B T , calcular el determinante de B (0,8 puntos).
c)
Obtener los
elementos de la matriz B considerada en el apartado b) (1,2
puntos).
PROBLEMA 2. Dados los puntos A = (4, -4, 9); B = ( 2, 0, 5); C = (4, 2, 6); L = (1, 1, 4); M = (0, 2, 3); y N
= (3, 0, 5), se pide:
a)
Calcular la
distancia d del punto C al punto medio del segmento de
extremos A, B (0,5 puntos) y el área
S del triángulo de vértices A, B,
C (1
punto).
b)
Calcular las
ecuaciones implícitas del plano
π que pasa por los puntos A,
B, C (0,4 puntos) y del plano
π’ que pasa por los puntos
L, M, N (1 punto).
c)
Calcular la
ecuación paramétrica de la recta r
intersección de los planos π y
π’ (0,6 puntos) y el ángulo α
que determinan los planos
π y π’
(0,4 puntos)
PROBLEMA 3. Dada la función
f(x) = ln x en el intervalo
cerrado [ 1 , e ], siendo e = 2,718281…:
a)
Razonar que
existe un punto P de la gráfica
y = ln x en el que la recta
tangente a ella es paralela a la recta que pasa por los puntos A = (1, 0)
y B = (e, 1) (1
punto).
b)
Obtener el
punto P considerado en a) (1,8 punto).
c)
Calcular la
pendiente de la recta tangente a y = ln
x en ese punto P (0,5
puntos).
PROBLEMA 4. El coste del marco de una ventana rectangular es
12,50 € por metro lineal de los lados verticales y 8 € por metro lineal de los lados
horizontales.
a)
Calcular
razonadamente las dimensiones que debe tener el marco de una ventana de 1 m3
de superficie para que resulte lo más económico posible (2,3
puntos).
b)
Calcular, además
el coste de ese marco más económico posible considerado en a) (1
punto).