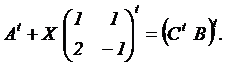Matemáticas aplicadas a las
Ciencias Sociales II Julio 2025 Reserva
BAREMO
DEL EXAMEN: Se
ha de contestar un problema del Apartado 1, un problema del Apartado 2 y el
problema del Apartado 3.
En cada cuestión se
indica la puntuación máxima, siendo la nota final la suma de las calificaciones
de cada una ellas. Se permite el uso de calculadoras siempre que no sean
gráficas o programables y que no puedan realizar cálculo simbólico ni almacenar
texto o fórmulas en memoria. Se utilice o no la calculadora, los resultados
analíticos, numéricos y gráficos deberán estar siempre debidamente
justificados. Está permitido el uso de regla. Las gráficas se harán con el
mismo color que el resto del examen.
Todas las respuestas han de estar debidamente
razonadas.
Apartado 1. Responda un problema de este
apartado de los dos propuestos.
Problema 1. A. Consideramos las matrices
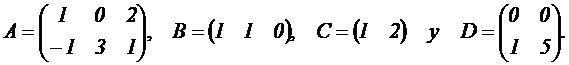
Sabiendo que, si K es una matriz, Kt representa su
matriz traspuesta, se pide:
a)
Calcular M =
A B t C – D. (0,75
puntos)
b)
Justificar
si M
es invertible y, si lo es, hallar su inversa. (0,75 puntos)
c)
Hallar M2 y M8. (0,5
puntos)
d)
Justificar
si son invertibles las matrices C C t y C
t C. (0,5
puntos)
|
e)
Hallar
la matriz X que satisface la
ecuación |
|
(1 punto) |
Problema 1.
B. Una empresa de organización de eventos desea poner a la venta dos tipos
de entradas para un evento musical: entradas preferentes y entradas estándar,
que se venden a 115€ y 90€, respectivamente, aunque en las localidades
preferentes la empresa tiene unos gastos de 5€ por entrada porque en ellas se
sirve un aperitivo. La instalación de cada localidad preferente tiene un coste
de 20€ y la de cada localidad estándar de 10€; la empresa dispone de un
presupuesto de 1.000€ para gastos de instalación. El aforo máximo es de 75
asientos.
a) ¿Cuántas entradas
de cada tipo se deben poner a la venta para obtener el máximo beneficio
posible? (3 puntos)
b)
¿Cuál es dicho
beneficio máximo? (0,5
puntos)
Apartado 2. Responda un problema de este
apartado de los dos propuestos.
Problema 2.
A. Una empresa agrícola que se dedica
al cultivo de frutas tropicales ha implementado un sistema de riego
automatizado para optimizar el consumo de agua. La función que describe la
necesidad de agua del cultivo (en m3/día) tras x días de crecimiento, para x entre 0 y 30, es:
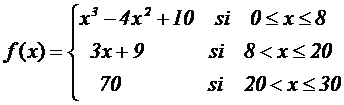
a)
Estudia
la continuidad de esta función en el intervalo [0,30].
(0´75 puntos)
b)
Determina
en qué días la necesidad de agua es máxima y mínima. (2 puntos)
c)
Calcula el área delimitada por esta función y
el eje OX entre los días 3
y 7. (0´75 puntos)
Problema 2.
B. Cuando la temperatura
de un invernadero se mantiene a x
grados centígrados, siendo x un
número real entre 10 y 30, la producción (en kilogramos) de cierta hortaliza
viene dada por la función Q(x) = 30 x2
+ A x + B − x3. Sabemos que la producción máxima se
alcanza cuando el invernadero se mantiene a 21 grados centígrados, y que dicha
producción máxima es 5.300 kg.
a)
Determina
los valores A y B que aparecen en la función Q(x).
(0,75 puntos)
b)
Determina los intervalos de crecimiento y
decrecimiento de la función Q(x). (1 punto)
c)
Para
valores de la temperatura comprendidos entre 10 y 30 grados centígrados, ¿en
algún caso se obtiene una producción inferior a 1.000 kg? (1 punto)
Apartado 3. Responda el único problema de este
apartado. (3 puntos)
Problema 3. Manuel va a celebrar su cumpleaños y ha invitado a dos
grupos de amigos que no se conocen entre sí: del instituto y de su barrio. Cada
grupo va a una tienda distinta a comprar un regalo. El grupo del instituto va a
la tienda A, donde un 40% de los regalos son libros, un 15% es ropa y un 45%
son juegos. El grupo de su barrio va a la tienda B, donde el 20% son libros, el
10% es ropa y el 70% son juegos. Supón que cada grupo elige aleatoriamente su
regalo. Calcula:
a) La probabilidad de que Manuel
tenga dos regalos de distinto tipo. (1
punto)
b) La probabilidad de que Manuel
tenga como regalo un libro o un juego. (1 punto)
c) La probabilidad de que, si
uno de los regalos es ropa y el otro no, el regalo de ropa se haya comprado en
la tienda A. (1 punto)