Matemáticas II Julio
2025
BAREMO DEL EXAMEN: Cada
problema se puntuará hasta 2,5 puntos.
La calificación del
ejercicio será la suma de las calificaciones de cada problema.
Se permite el uso de
calculadoras siempre que no sean gráficas o programables, y que no puedan
realizar cálculos simbólicos ni almacenar texto o fórmulas en memoria. Se
utilice o no la calculadora, los resultados analíticos, numéricos y gráficos
deberán estar siempre debidamente justificados.
A partir de la
tercera falta de ortografía se deducirán -0,10 puntos hasta un máximo de un
punto.
Por errores en la
redacción, en la presentación, falta de coherencia, falta de cohesión,
incorrección léxica e incorrección gramatical se podrá deducir un máximo de
medio punto.
En las
respuestas se deben escribir todos los pasos del razonamiento utilizado.
PREGUNTA 1: PROBABILIDAD
Y ESTADÍSTICA (2,5 puntos)
La empresa TikiTak ha
realizado un estudio del comportamiento de sus usuarios y ha observado que las
3/5 partes de sus publicaciones reciben un “Like”. Juana es una usuaria de
TikiTak. Se pide:
1.1 (0.75 puntos) ¿Cuál es la
probabilidad de que Juana no reciba ningún “Like” si ha subido a la plataforma
TikiTak cuatro publicaciones?
1.2 (0.75 puntos) ¿Cuál es la
probabilidad de que Juana no reciba más de dos “Likes” en sus cuatro
publicaciones?
1.3 (1
punto) Juana desea que la probabilidad de recibir al menos un “Like” sea
mayor que 0.999. ¿Cuál es el menor número de publicaciones que ha de subir para
conseguirlo?
PREGUNTA 2: ÁLGEBRA (2,5 puntos)
Responda al apartado 2.1 o al apartado 2.2
2.1 Se dan las
matrices
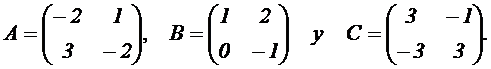
Obtener:
|
2.1.1 (1.25 puntos) La matriz X solución de la ecuación |
|
|
|
2.1.2 (0.5 puntos) El determinante de la
matriz |
|
|
2.1.3 (0.75 puntos) Los valores de a y b, si existen, tales que a B100
+ b B99 = A + C.
___________________________________________________________________
2.2 Se considera el siguiente sistema de ecuaciones
lineales que depende del parámetro real a:
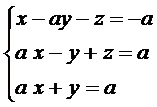
Se pide:
2.2.1
(1.25 puntos) Discutir el sistema de ecuaciones en función de los valores del parámetro a.
2.2.2
(1.25 puntos) Calcular el conjunto de soluciones del sistema para
aquellos valores de a para los que el sistema es
compatible determinado.
PREGUNTA 3: GEOMETRÍA (2,5 puntos)
Responda al apartado 3.1 o al apartado 3.2
3.1 Dados los planos
p1: x + 2 y + m
z = – 1, donde m es
un parámetro real, y p2: x + z = 6.
3.1.1 (0.5 puntos) Encontrar
el valor de m, si existe, para el que p1 y p2 son
perpendiculares.
3.1.2 (1.25 puntos)
Encontrar el valor de m
para el que p1 y p2 forman un
ángulo de 45 grados.
3.1.3 (0.75 puntos) Calcular la ecuación
paramétrica de la recta intersección de p1 y p2.
___________________________________________________________________
3.2 Dado el plano p: 3 x + y – z = 2 y
los puntos P = (0, 1, – 1) y Q =
(1, a, 1), calcular:
3.2.1 (1.25 puntos) Los valores del parámetro a,
si existen, para los que la recta que pasa por
P y Q
está contenida en el plano p.
3.2.2 (1.25
puntos) Para a =
1, el punto simétrico de Q respecto del plano π.
PREGUNTA 4: ANÁLISIS (2,5 puntos)
Responda al apartado 4.1 o al apartado 4.2
4.1 Dada la
función real de variable real
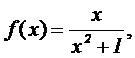
se pide:
4.1.1 (0.5 puntos) Hallar
el dominio, las asíntotas y los intervalos de crecimiento y decrecimiento de la
función f.
4.1.2
(1.5 puntos) Calcular, si existen,
los valores máximos y mínimos relativos y absolutos de la función f.
4.1.3 (0.5 puntos) Representar la función f.
___________________________________________________________________
4.2 Dadas las
funciones reales de variable real
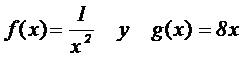
Se pide:
4.2.1 (0.5 puntos) Hallar
el dominio, las asíntotas y los intervalos de crecimiento y decrecimiento de la
función f.
4.2.2 (0.25 puntos) Dibujar las gráficas de
ambas funciones.
4.2.3 (1.75 puntos) Calcular el área del
recinto delimitado por el eje de
abcisas, la rectas x = 1 y las gráficas de las dos funciones y =
f(x) e
y = g(x).