Matemáticas aplicadas a las
Ciencias Sociales II Julio 2024
BAREMO
DEL EXAMEN:
Se
han de contestar tres problemas de entre los seis propuestos.
Cada problema se valorará de
Se permite el uso de calculadoras siempre
que no sean gráficas o programables, y que no puedan realizar cálculo simbólico
ni almacenar texto o fórmulas en memoria. Se utilice o no la calculadora, los
resultados analíticos, numéricos y gráficos deberán estar siempre debidamente
justificados. Está permitido el uso de regla. Las gráficas se harán con el
mismo color que el resto del examen.
Todas las respuestas han de estar debidamente
razonadas.
Problema 1. Una fábrica vende
diariamente dos modelos de bolígrafos de color verde. El modelo sencillo
requiere una unidad de tinta y otra de plástico para su fabricación, el más
sofisticado requiere una unidad de tinta y una y media de plástico. Dispone de 2500
unidades de tinta y de 3000 de plástico, y además se sabe que no se pueden fabricar
más de 2000 unidades de bolígrafos sencillos. Por cada bolígrafo sencillo la
empresa gana 0,5 euros y por cada uno de los sofisticados 0,7 euros.
a)
¿Cuántas unidades
de cada tipo debe producir para maximizar las ganancias? (8
puntos)
b)
¿A cuánto
ascienden estas ganancias máximas? (2
puntos)
Problema 2. Consideramos las
matrices
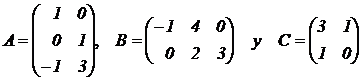
a)
Analiza si la
matriz A B – 2 I es invertible,
siendo I
la matriz identidad de orden 3.
(3 puntos)
b)
Determina la matriz X que es
solución de la ecuación A + 2 X C = Bt, siendo Bt la matriz traspuesta de la matriz B. (4
puntos)
|
c) Calcula para qué valores de
z la matriz
|
|
cumple la condición |
C D = D C. (3 puntos)
|
Problema 3.
Se considera la función |
|
Se pide: |
a)
Su dominio y los puntos
de corte con los ejes coordenados. (2 puntos)
b)
Las asíntotas
horizontales y verticales, si existen. (2 puntos)
c)
Los intervalos de
crecimiento y decrecimiento. (2 puntos)
d)
Los máximos y
mínimos locales, si existen. (2 puntos)
e)
La representación
gráfica de la función a partir de los resultados anteriores. (2 puntos)
Problema 4. Un agricultor estima que si aplica x kilos de abono en un terreno, sus ingresos
serán – x2 + 60 x +
100 euros.
a)
¿Qué cantidad de
abono maximiza sus ingresos? ¿Cuáles son estos ingresos máximos? (3
puntos)
b)
Si el coste del
abono es de 12 euros por kilo, ¿qué cantidad de abono maximiza sus beneficios?;
¿cuáles son estos beneficios máximos? (4 puntos)
c)
¿Qué cantidades
de abono garantizan beneficios positivos? (2 puntos)
Problema 5. Un
instituto tiene estudiantes de ESO y de Bachillerato. El instituto ofrece tres
extraescolares: dos deportivas (fútbol y baloncesto) y una no deportiva
(música); todos los estudiantes tienen que escoger una extraescolar, pero solo
una. El instituto tiene en total 400 estudiantes, y 300 de ellos han escogido
fútbol. El instituto tiene 310 estudiantes de ESO; de ellos, 230 han escogido
fútbol y 60 han escogido baloncesto. Se sabe también que 8 estudiantes de
Bachillerato han escogido música. Seleccionamos al azar un estudiante de este
instituto.
a)
Calcula la
probabilidad de la unión de los sucesos “el estudiante está en ESO” y “el estudiante
ha escogido música”. (3 puntos)
b)
Si sabemos que el
estudiante seleccionado ha escogido una extraescolar deportiva, ¿cuál es la
probabilidad de que esté en ESO? (4 puntos)
c)
¿Son
independientes los sucesos “el estudiante está en Bachillerato” y “el estudiante
no ha escogido baloncesto”? (3 puntos)
Problema 6. Una empresa de vacunas para ganado bovino está evaluando la
efectividad de dos métodos distintos, A y B, para administrar una vacuna contra
virus que afectan al aparato respiratorio. En el estudio, de las 600 reses de
una explotación ganadera, 250 fueron vacunadas por el método A, otras 250 por
el método B y el resto no fueron vacunadas. Se observó que en los cuatro meses
siguientes tuvieron problemas respiratorios el 30% de las reses vacunadas por
el método A, el 20% de las vacunadas por el método B y el 60% de las no
vacunadas. Calcula:
a)
La probabilidad
de que una res elegida al azar haya tenido problemas respiratorios.
(3 puntos)
b)
La probabilidad
de que una res que no ha tenido problemas respiratorios haya sido vacunada por
el método B. (4
puntos)
c) La probabilidad de la intersección de los sucesos “la
res no ha sido vacunada” y “la res tiene problemas respiratorios”. (3 puntos)
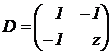
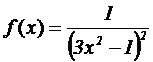 .
.