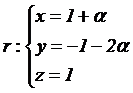Matemáticas II Julio
2025 Extra
BAREMO DEL EXAMEN: Cada
problema se puntuará hasta 2,5 puntos.
La calificación del
ejercicio será la suma de las calificaciones de cada problema.
Se permite el uso de calculadoras
siempre que no sean gráficas o programables, y que no puedan realizar cálculos
simbólicos ni almacenar texto o fórmulas en memoria. Se utilice o no la
calculadora, los resultados analíticos, numéricos y gráficos deberán estar
siempre debidamente justificados.
A partir de la
tercera falta de ortografía se deducirán 0,10 puntos hasta un máximo de un
punto.
Por errores en la
redacción, en la presentación, falta de coherencia, falta de cohesión,
incorrección léxica e incorrección gramatical se podrá deducir un máximo de
medio punto.
En las
respuestas se deben escribir todos los pasos del razonamiento utilizado.
PREGUNTA 1: PROBABILIDAD
Y ESTADÍSTICA (2,5 puntos)
Los vuelos que llegan a un
aeropuerto se clasifican en tres grupos: vuelos puntuales, vuelos con retrasos
de hasta tres horas y vuelos con retrasos de más de tres horas. La puntualidad
de los vuelos se ve afectada por las condiciones meteorológicas del momento. Si
las condiciones meteorológicas son buenas, el porcentaje de los vuelos que llegan
con puntualidad es del 70% mientras que el 10% llegan con más de tres horas de
retraso. Si las condiciones meteorológicas son malas, el porcentaje de los
vuelos que llegan con puntualidad es del 40% mientras que el 30% llegan con más
de tres horas de retraso. Se calcula que el 90% de los días las condiciones meteorológicas
son buenas.
1.1
(0.5 puntos) ¿Cuál es la
probabilidad de que un vuelo llegue con más de 3 horas de retraso?
1.2
(1 punto) Sabiendo que un vuelo
ha sido puntual, ¿cuál es la probabilidad de que las condiciones meteorológicas
fueran malas?
1.3 (1 punto) Un pasajero realiza un vuelo a dicho aeropuerto, desde donde debe tomar otro vuelo a su destino final. Este segundo vuelo enlaza si el primero llega con 3 horas o menos de retraso. Si realiza este viaje una vez al mes durante un año y viaja siempre en condiciones meteorológicas buenas ¿cuál es la probabilidad de que pueda enlazar con el vuelo a su destino final en todos sus viajes?
PREGUNTA 2: ÁLGEBRA (2,5 puntos)
Responda al apartado 2.1 o al apartado 2.2
2.1 Se considera la matriz
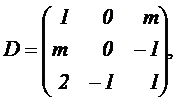
que
depende del parámetro real m, y las matrices
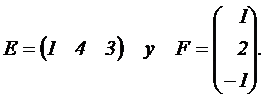
Se pide:
2.1.1 (0.5 puntos) Indicar, si existen, los valores del
parámetro m para los que D tiene inversa.
|
2.1.2 (1 punto) Calcular las matrices E F y (F E )t, si existen. |
|
2.1.3
(1 punto) Resolver, para m = 0, la ecuación matricial con
incógnita X:
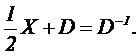
___________________________________________________________________
2.2 Dada la matriz
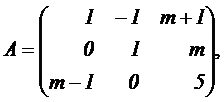
2.2.1
(1.25 puntos) Estudiar el rengo de
la matriz A en función del parámetro real m.
|
2.2.2
(1.25 puntos) Para m = 0, calcular la matriz inversa de |
|
,
si existe. |
PREGUNTA 3: GEOMETRÍA (2,5 puntos)
Responda al apartado 3.1 o al apartado 3.2
3.1 Dados los
planos p1: 2 x – a2 y – a z = a – 1 y p2: (a – 1) x –
a y – z = a, se pide:
3.1.1 (1.5 puntos) Estudiar
en función de a si los planos anteriores
coinciden, son paralelos no coincidentes o se cortan.
3.1.2 (0.5 puntos) Calcular,
para a
= 0, el ángulo entre los planos p1 y p2.
3.1.3 (0.5 puntos) Calcular,
para a
= 0, la distancia del punto P = (1, 0, – 1) y el plano p1.
___________________________________________________________________
|
3.2 Dado
el plano p: 2 x + y – 3 = 0
y la recta |
|
, se pide: |
3.2.1 (1.25 puntos) Obtener la ecuación del
plano perpendicular a p y que contiene
a r.
3.2.2 (1.25
puntos) Calcular, si existe, un plano
paralelo a π y que contenga a r.
PREGUNTA 4: ANÁLISIS (2,5 puntos)
Responda al apartado 4.1 o al apartado 4.2
4.1 Dadas las
funciones f(x) = x4 – 7 x2 + 16 y g(x) = x2, obtener:
4.1.1 (1.25 puntos) Los intervalos de crecimiento y
decrecimiento, y los extremos relativos de de la función
y = f(x).
4.1.2
(1.5 puntos) El área de la
superficie finita encerrada entre las curvas
f(x) y g(x).
___________________________________________________________________
4.2 Una
costa marítima se extiende en línea recta hacia la derecha desde un punto P de
la costa. A 8 km de P hay una refinería situada en la costa. Además, hay una
plataforma petrolífera en el mar que está situada a 6 km de distancia de P en
la recta perpendicular a la costa desde el punto P. Se construirá un oleoducto desde
la plataforma hasta la refinería. El coste de construir el oleoducto bajo el
agua es de 1 millón de euros por kilómetro y el de construirlo sobre tierra, de
0,6 millones de euros por kilómetro.
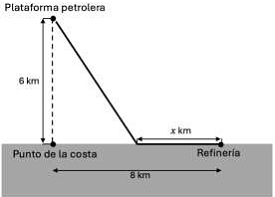
4.2.1
(0.5 puntos) Encontrar la función
del coste de construcción del oleoducto dependiendo de la distancia, x, entre
el primer punto donde el oleoducto toca la costa y la refinería.
4.2.2 (1.5 puntos) Encontrar
el valor de x para que el coste de construcción del oleoducto sea mínimo.
4.2.3 (0.5 puntos) Calcular
dicho coste.